민스씨의 일취일장
Java | 백준 11057 오르막 수 본문
백준 11057 오르막 수 문제에 대한 글입니다.
백준 11057 오르막 수

문제
문제 정보는 아래 링크에서 확인할 수 있다.
11057번: 오르막 수
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다. 예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다. 수
www.acmicpc.net
접근 방법
규칙이 있는 수의 나열 및 경우의 수는 이전의 결과가 다음 결과에 규칙적으로 영향을 준다. 따라서 이와 같은 문제는 바로 직전에 영향을 주는 필수 요소를 찾고, 가장 처음부터 값을 쌓아 나가야 한다. 핵심 키워드는 점화식과 초기조건이다.
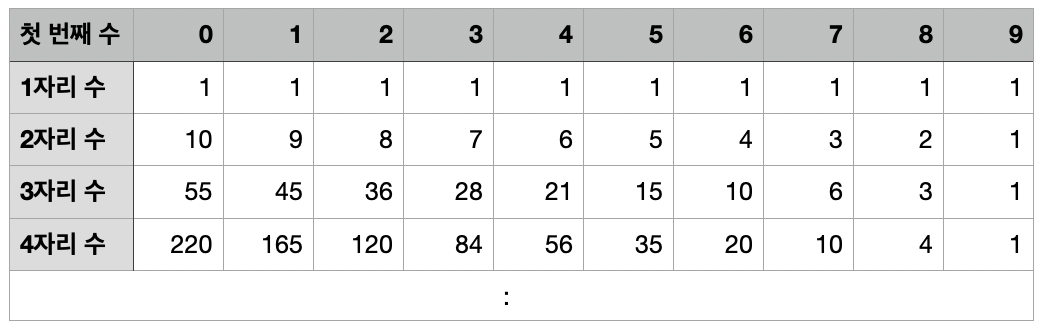
첫 번째 수 : 수의 첫 번째 수가 어떤 수인지 알려준다. (0부터 수가 시작할 수 있다.)
1 자리 수 : 첫 번째 수에 대해서 1자리 수의 경우의 수는 몇 개인지 각각 표기 된 것이다. 하여 전체 1자리 수의 경우의 수는 1자리 수 행의 전체 합과 같다.
2 자리 수: 첫 번째 수에 대하여 2자리 수의 경우의 수가 각각 몇 개인지 표기 된 것이다. 역시 전체 2자리 수의 경우의 수는 2자리 수 행의 전체 합과 같다.
규칙 : N자리 수의 경우의 수는 N+1자리 수의 첫 번째 수가 0인 경우의 수와 같다. 따라서 구하는 자리 수의 경우의 수는 다음 자리수의 첫 번째 수가 0인 경우의 수를 찾으면 된다.
전체 코드
public class baekjoon11057 {
static Scanner sc = new Scanner(System.in);
static int N;
static int[][] dpGraph;
static void input() throws IOException{
N = sc.nextInt();
dpGraph = new int[N+1][10];
for(int i=0; i<10; i++){
dpGraph[0][i] = 1;
}
for(int i=1; i<=N; i++){
dpGraph[i][9] = 1;
}
}
static int execute(){
for(int i=1; i<=N; i++){
for(int j=8; j>=0; j--){
dpGraph[i][j] = (dpGraph[i-1][j] + dpGraph[i][j+1])%10007;
}
}
return dpGraph[N][0];
}
public static void main(String[] args) throws IOException {
input();
System.out.println(execute());
}
}소감
정말 재미있는 문제이다. 이 문제를 분명히 8개월 전 쯤에도 한 번 봤었다. 그 당시엔 풀지 못했다. 다른 사람들의 풀이를 봤을 때, 왜 표를 이용해서 풀어야 하는지, 나는 다르게 풀 수 있지 않을까 하는 고집스런 마음도 있었다. 그렇게 못 푼 문제로 남아 있었는데, 오늘 다시 마주하였다. 이번에도 수학적인 접근을 코드로 풀어내는 데 한계를 느껴, 다른 사람들의 풀이를 참고하였다. 여러 사람들의 접근을 보며 왜 표로 풀어야 하는지 그리고 얼마나 이 방법이 프로그래밍 적으로 유용한지 느낄 수 있었다.
- 가장 큰 특징은 머릿 속에서 복잡하고 다방향으로 풀던 수학 문제를 2차원 평면위로 풀어 놓았다는 점이다. 평소 생각하던 방식과 다른 접근이기 때문에 낯설로 번거롭게 느껴졌지만 단순화(도식화)한 표가 복잡한 수학 문제를 얼마나 프로그램적(단방향 연산)으로 해결하는데 도움을 주는 지 알게 되었다. 더불어 그 동안 복잡하게만 생각하려 했던 나 자신을 되돌아 보는 계기가 되었다.
- 이 방법을 이용한다면 많은 문제를 생각하던 것 보다 훨씬 간단하게 풀어낼 수 있겠단 생각이 들었다.
- "수학"이 원리를 깊게 찾아 나서는 여정이라면, "컴퓨터 공학"이라는 분야는 그 복잡한 수학을 응용가능한 형태로 만드는 역할을 한다는 생각이 들었다. (정말 매력적이다.)
'Data Structure & Algorithm > Java' 카테고리의 다른 글
| Java | 백준 2667 단지번호 붙이기 (0) | 2024.02.09 |
|---|---|
| Java | 백준 11724 연결 요소의 개수 (0) | 2024.02.08 |
| Java | 백준 26169 세 번 이내에 사과를 먹자 문제풀이 및 분석 (0) | 2024.02.08 |
| Java | 백준 1388 바닥 장식 문제풀이 및 분석 (0) | 2024.02.07 |
| Java | 백준 13300 방배정 풀이 전략 기록 (0) | 2023.08.09 |




